| View previous topic :: View next topic |
| Author |
Message |
ZeroAssoluto
Joined: 05 Feb 2017
Posts: 994
Location: Rimini, Italy
|
 Posted: Wed Sep 01, 2021 8:42 am Post subject: Sep 01 VH Posted: Wed Sep 01, 2021 8:42 am Post subject: Sep 01 VH |
 |
|
Hi everyone,
| Code: |
+------------+-------------+--------------+
| 258 9 1258 | 3 16 15 | 4678 46 47 |
| 58 7 158 | 169 4 159 | 68 2 3 |
| 3 4 6 | 2 8 7 | 9 1 5 |
+------------+-------------+--------------+
| 278 1 278 | 5 29 3 | 47 49 6 |
| 9 5 4 | 67 67 8 | 2 3 1 |
| 6 3 27 | 19 129 4 | 5 8 79 |
+------------+-------------+--------------+
| 1 2 9 | 4 5 6 | 3 7 8 |
| 457 8 57 | 179 3 129 | 146 469 249 |
| 47 6 3 | 8 179 129 | 14 5 249 |
+------------+-------------+--------------+
|
Play this puzzle online at the Daily Sudoku site
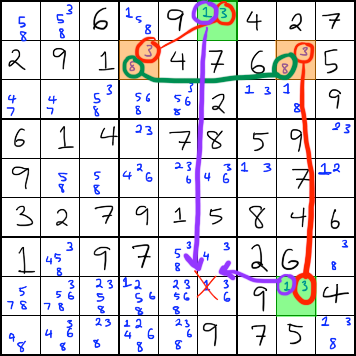
XY-Wing 4,7,9 in r16c9,r4c8 and -4 in r1c8
Ciao Gianni |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Wed Sep 01, 2021 9:49 am Post subject: Posted: Wed Sep 01, 2021 9:49 am Post subject: |
 |
|
Since I learnt that the VH puzzles can be solved with X,XY or XYZ that's what I try to look for, maybe not so successfully.
What I saw was r8c8 <> 6 as then r89c7 = 14 and r1c8= 4 leading to no 4's in box 6 |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Sep 01, 2021 2:07 pm Post subject: Posted: Wed Sep 01, 2021 2:07 pm Post subject: |
 |
|
That's a nice ANP, Tom (Almost Naked Pair) based around the <146> at r89c7.
Simply put - either the naked pair <14> is true or the "fin" 6 is true.
Whatever, there can be no 6 in r8c8.
Here's the forcing chain:
(6=14)r89c7-(4)r4c7=r4c8-(4=6)r1c8 ==> r8c8<> 6
Last edited by Mogulmeister on Wed Sep 01, 2021 4:05 pm; edited 1 time in total |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Wed Sep 01, 2021 2:26 pm Post subject: Posted: Wed Sep 01, 2021 2:26 pm Post subject: |
 |
|
Mogulmeister, thanks for letting me know what I'm doing!
Another way to solve could be r89c7 <>4 as then r4c7=7, r6c9=9 leads to only 2's in r89c9 |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Sep 01, 2021 3:50 pm Post subject: Posted: Wed Sep 01, 2021 3:50 pm Post subject: |
 |
|
...and that is your contradiction loop which is the same chain as above but extended one more step. The <> 6 in r8c8 creates a 249 triple (in red) which removes both the 4's at the start point!
(6=14)r89c7-(4)r4c7=r4c8-(4=6)r1c8-(6=49|249|249)r8c89,r9c9 ==>
r89c7<>4 |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Wed Sep 01, 2021 5:04 pm Post subject: Posted: Wed Sep 01, 2021 5:04 pm Post subject: |
 |
|
I understand the forced chain of my first solution, but not sure about this explanation.
| Mogulmeister wrote: | ...and that is your contradiction loop which is the same chain as above but extended one more step. The <> 6 in r8c8 creates a 249 triple (in red) which removes both the 4's at the start point!
(6=14)r89c7-(4)r4c7=r4c8-(4=6)r1c8-(6=49|249|249)r8c89,r9c9 ==>
r89c7<>4 |
My second solution does not require the <> 6 in r8c8 to work
r89c7 <>4 as then r4c7=7, r6c9=9 leads to only 2's in r89c9
or
r89c7 <>4 as then r89c9=29, r6c9=7, r4c7=4 |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Sep 01, 2021 7:02 pm Post subject: Posted: Wed Sep 01, 2021 7:02 pm Post subject: |
 |
|
What I was doing Tom was extending your first forcing chain by a single step and creating the general contradiction loop. I was taking the line of least resistance from your former structure to get the same result. An extension of your original idea.
There are multiple contradictions that all create the eliminations of the two 4's. This stems from the fact that we have plugged 4 into the start at r89c7. These are all kicking off at once.
Last edited by Mogulmeister on Wed Sep 01, 2021 7:20 pm; edited 1 time in total |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Wed Sep 01, 2021 7:17 pm Post subject: Posted: Wed Sep 01, 2021 7:17 pm Post subject: |
 |
|
Your two:
(6=14)r89c7-(4=7)r4c7-(7=9)r6c9-(9=24|24)r89c9 ==> r89c7 < >4
(6=14)r89c7-(4=29|29)r89c9-(9=7)r6c9-(7=4)r4c7 ==> r89c7 < >4 |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Thu Sep 02, 2021 7:38 am Post subject: Posted: Thu Sep 02, 2021 7:38 am Post subject: |
 |
|
Thanks, Mogulmeister this helps me move forward with sudoku (especially eureka, but I'm not there yet!)
Going back to my first solution (ANP) I thought this was also an XY chain with r1c8 and r8c7 being pincers on 6 which would remove the 6 in r12c7 and r8c8
On my second try you have turned this into two different solutions but to my mind it's only the direction that changes - clockwise or anticlockwise
iechyd da |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Thu Sep 02, 2021 8:47 am Post subject: Posted: Thu Sep 02, 2021 8:47 am Post subject: |
 |
|
Yes. An xy chain is traditionally a series of linked bivalues- only two candidates per cell. Hence the “xy”.
That’s just terminology.
However, as you said, the pincer idea is the most important one and how they are connected is what matters.
How did you link the 6s in r1c8 and r8c7 ?
Last edited by Mogulmeister on Thu Sep 02, 2021 9:44 am; edited 1 time in total |
|
| Back to top |
|
 |
TomC
Joined: 30 Oct 2020
Posts: 358
Location: Wales
|
 Posted: Thu Sep 02, 2021 9:14 am Post subject: Posted: Thu Sep 02, 2021 9:14 am Post subject: |
 |
|
My thought process was
if r1c8 = 6 then it eliminates
if r1c8 = 4 then r4c7=4, r9c7=1, r8c7=6
so either 6 is in r1c8 or r8c7
I didn't use the 79 in box 6 but if I did then maybe it is an XY chain |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Thu Sep 02, 2021 11:05 am Post subject: Posted: Thu Sep 02, 2021 11:05 am Post subject: |
 |
|
It’s only “a quasi xy” if you include the 79 in box 6 because of the tri value at r8c7. However, none of this matters a whole lot since the fundamental pincer op works via strong links and you don’t need the 79. All good.
The contradiction loop uses the same pathway but the direction of travel matters. Clockwise, the 4’s in r89c7 are eliminated via the <24> pair. Anti-clockwise the 4’s are eliminated by the 4n r4c7. |
|
| Back to top |
|
 |
Mogulmeister
Joined: 03 May 2007
Posts: 1151
|
 Posted: Thu Sep 02, 2021 11:29 am Post subject: Posted: Thu Sep 02, 2021 11:29 am Post subject: |
 |
|
Did you see the mutant xy wing on steroids ?
Consider r4c7 - r6c9 - r89c9 as the mutant or double finned XY wing.
If r4c7 = 4 then it eliminates the 4s in r89c7.
If not then r4c7 = 7 and r6c9= 9 and r89c9 = locked pair <24> which eliminates the 4s in r89c7.
Eureka
(4=7)r4c7-(7=9)r6c9-(9=24|24)r89c9
r89c7 <> 4 |
|
| Back to top |
|
 |
|



