Nurikabe @ Daily Sudoku


Nurikabe @ Daily Sudoku
|

|
Let's work through an example Nurikabe problem. This one is quite straightforward. At any stage below, click the grid for a printable grid.
Nurikabe has 4 rules:

First look at the number 1 close to the center of the puzzle. Remember, each island must contain just one number. The number 1 represents an island with only 1 white square, so we can shade the surrounding squares. The same is true for the number 1 in the top right corner.
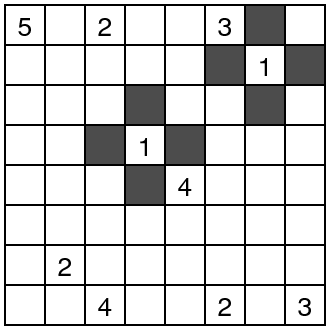
No group of white squares may contain more than one number. This means that numbers must be separated by shaded squares. When we have two numbers with one one square between them, that square must be shaded. For example, the 5 and 2 in the top left corner must be separated by a black square.

Concentrate now on the bottom left corner of the grid. Every black square must be connected to form the "wall". The black square in the bottom left corner must not be isolated. It only has one available neighbour, which must therefore be black. Where there is only one possibility, we must extend the wall.

Take a look at the number 2 in the bottom left corner. This island is not yet complete -- it needs a second white square. The number now has only one available neighbour, which must therefore be white. We can put a dot in that square to show that it must be white. The "2" island is now full, and so must be surrounded by black squares.

Take a look at the squares marked with (a). These squares are surrounded, and therefore cannot be part of any island. They must be shaded.
While we're there, we must extend the wall in the top right corner. Look for other spots where the wall must be extended.

Take a look at the 5 in the top left corner. We need to extend the island. Use dots to show which squares must be white.
Which other islands can be extended?

Rule 4 says that 2x2 blocks of filled squares are disallowed. The two squares marked (a) in the left center of the grid must be white, because shading them would violate this rule. Mark them with dots.

In step 2, we filled squares that were separating two numbers. We can extend this logic to fill squares that separated growing islands. Look at the squares marked (a). Do you understand why they must be shaded?

The most common mistake is to focus only on the wall, or only on the islands. You need to swicth from one to the other and back. See if you can extend parts of the wall to stop them becoming isolated, and extend islands and shade around them when they are full.

You're nearly done! Note in the grid shown here, we must fill the squares marked (a) so as not to isolate chunks of the wall.

The remaining islands can be extended in only one direction. The final shaded square links two large sections of wall into one continuous unit.

Well done! Now take a look at some of the puzzles available on the puzzles page. Remember:
| All content © The Daily Sudoku Ltd 2005-2025. All rights reserved. | Comments, questions, problems? |